Most switching power conversion circuits use magnetic devices to help perform their function. Even “linear” power supplies often use a transformer as an impedance converter and dielectric isolation device. Strictly speaking, transformers aren’t energy storage devices and therefore won’t be considered directly in this discussion.
INDUCTORS
Whenever an electric current flows, it produces a magnetic field. The higher the current, the stronger the field. This magnetic field stores energy, whether you want it to or not. This property of storing energy is called Inductance and is measured in units named Henrys (H) . Inductance can be increased for a given length of wire by winding the wire into a coil. The magnetic field produced by each turn interacts with the field of other turns and multiplies the effect, causing the inductance of a coil of wire to increase by the number of turns (N) squared. Therefore, if you double the number or turns, you quadruple the inductance. Whenever you see a coil of wire, some engineer was trying to get more inductance into a smaller space using less wire. Or he needed to get rid of some extra wire and didn’t care about the extra inductance. I have always found energy stored in an inductor to be a very strange thing. Magnetic energy storage is easily described with math, but that doesn’t make it any easier to “feel” how it works. There is an analogy that gives me a better grip on this storage phenomenon; a flywheel. Try this and see if it works for you. Imagine a flywheel with perfect bearings spinning in a vacuum. If left undisturbed it will continue to spin forever. The mechanical energy stored is mv**2 / 2, where m is the effective mass of the flywheel and v is the velocity (rpm). For an inductor, the energy stored (in Joules) is LI**2 / 2, where L is the inductance in Henrys and I is the current in Amperes. Notice the direct correlation in the equations between the units of mass-inductance and velocity-current. The inductive equivalent of “frictionless bearings in a vacuum” is wire with no resistance. Such wire actually exists; it’s called a superconductor. But usually the inductors in power supply circuits have a series resistance and therefore “friction”. If you get a current flowing in an inductor and then short the two ends together the current will go to zero with a Time Constant of L/R, where R is the resistance of the wire. Note that if the R is zero, the current never changes (TC is infinity). So how does this analogy actually work? Well, if you try to stop a spinning flywheel by using friction, the result after the wheel stops is heat. If you let the current in a real inductor (with resistance) circulate until it’s zero you also get heat. If you try to stop a spinning flywheel suddenly, there are huge forces generated and things break. If you open the circuit of an inductor with current flowing you get very large voltages and sometimes an arc or cooked components. In each case you are trying to remove a finite amount of energy from a storage system in zero time. That requires an infinitely large force (in the flywheel) or Voltage (in the inductor). Both are bad. Once you start current flowing in an inductor, always have some place for the energy to go when you try to reduce the current. Simple, but very important. Here’s another one; The velocity of a flywheel after a very short period of time is almost the same as the velocity before that time. Another way of saying that it is very difficult to change the velocity over short time periods. Likewise, it is difficult to change the current flowing in an inductor quickly. Enough of the analogies, back to actual components.
A way to get even more inductance in a given volume is to insert a piece of ferromagnetic material into the inductor (coil of wire). Ferromagnetic materials have molecules (or atoms) that have a net dipole moment and therefore act like little permanent bar magnets. The magnetic field from the coil pulls on these little magnets and causes them to line up with the field. This effectively amplifies the field of the coil and causes the inductance to be higher than it would otherwise be. If you remove the external field, the dipoles will snap back toward their original (unaligned) position leaving little or no residual magnetism in the material. Powdered iron and ferrites are two common classes of ferromagnetic materials that could be used to make power inductors. So the ferromagnetic material has the property of increasing the stored energy of the inductor for a given current and N. Different ferromagnetic materials have different abilities to increase the inductance. The ratio of inductance with a material in the coil versus vacuum is called the permeability of the material. Vacuum (or aether, as it is known in Canada) is defined to have a permeability of one. Some materials have a permeability in the thousands. Sound too good to be true? Well, it is true, but…. Let’s go back to the little bar magnet analogy. Increasing the current in the coil causes a larger magnetic field inside the coil, which pulls harder on the little magnets. At some magnetic field intensity, all of the little magnets will have lined up with the external field. Increasing the field beyond this point won’t cause the magnets to move any further and therefore won’t add any additional field strength. This means the small signal inductance is now back to what it would be if no ferromagnetic material were in the coil. This condition is described as saturated. All permeable core inductors have a maximum current beyond which they will saturate. The bad news is that materials with higher permeability saturate with less applied magnetic field, often making them less desirable as inductor cores. Most power inductors have effective core permeability in the 100 range. Since saturation usually happens in a messy, non-linear way, power storage inductors are usually operated below about 80% of their saturation current. But wait, there’s more! (non-ideal properties, that is). Using that handy little bar magnet analogy again, imagine that the magnets are submerged in a liquid. Every time you torque the magnets with the external field, you stir the liquid. This takes energy and causes things to warm up. The amount of energy lost verses time is proportional to how fast and how far you move the magnets. The higher the current and the higher the frequency, the higher th losses. Finally, there is the resistance of the wire in the coil. Inductors have "I squared R" losses, just like resistors do. And don’t think you can escape by making the wire bigger in diameter. First, you can’t get as many turns of big wire on a given size core. If you increase the core size, you increase the volume of magnetic material and therefore the losses for a given field in the core, see above. Even worse, at higher frequencies the impedance of the wire doesn’t drop as much as the cross sectional area increase would imply. That’s because more current per unit area flows in the outer “skin” of the wire than in the center. No, really, I’m not kidding. It’s called “skin effect” and is very real at the frequencies used in modern switchers. Inductor design is always a tradeoff of cost, size, weight and efficiency. So we have two mechanisms that generate heat (three with skin effect) and one that limits the maximum current we can use. There are actually even more problems at higher frequencies, but leave that to the RF guys.
So why would anyone want to use these hot, heavy, non-linear parts in their design? Because they store energy and have a high impedance at high frequencies. This combination of properties is just too useful to ignore.
ENERGY STORAGE
Current in an inductor generates a magnetic field and the magnetic field is where the energy is stored. Therefore it makes sense that the amount of energy stored is a function of the current and inductance. In algebraic notation:
Energy = [ L x I**2] / 2 , where L is in Henrys, I is in Amps, and Energy is in Joules
Remember that the energy you get back out of an inductor will be less than the formula shows because of the loss mechanisms discussed above. Inductors always heat up when you move current through them. To start or stop a current in an inductor you need to apply a voltage across its terminals. Theory says that the current in a (lossless) inductor increases linearly with time if a constant voltage is applied:
I = (V x deltaT)/ L
This formula says that the current (I) will get very large if time (deltaT) is very long. In practice, there is always a current limiting element somewhere in the circuit, often it is the resistance of the wire in the inductor. This resistance sets the maximum current that will flow in the inductor, even after infinite time. That maximum current is often above the saturation point and might be in the “smoke region”. The voltage across the inductor can also be described as the “change in current verses time”:
V = L di/dt
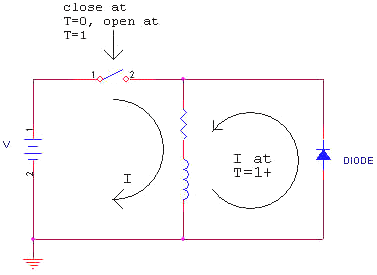
This formula has an interesting consequence. It says that if you try to vary the current flow very quickly, the voltage across the inductor will get very large. If you put a mechanical switch in series with an inductor that has current flowing in it and then open the switch, the current doesn’t stop flowing. The voltage simply rises until the current arcs across the switch terminals (or the inside of the inductor!). This can be bad news for both mechanical and semiconductor switches. A series RC network called a snubber is often placed across a switch in this application. Another consequence of this formula is that if the voltage across a lossless inductor is reduced to zero while a current is flowing, the current will remain constant with time. This is how superconducting magnets store energy with no loss. So, how can we use an inductor in a switched circuit? The answer is to always have a circuit path for the inductor current to flow. Look at the figure below. The switch is closed at T=0 with no current flowing in the inductor. At time T=1 there is a current I in the inductor and the switch is opened. The current will not change instantaneously so the voltage at the top of the resistor will fall rapidly (with respect to the bottom of the inductor) until the diode becomes forward biased. Now the current has a path to flow and the algebra is happy. The current will continue to flow until I**2R losses in the resistor and the IV losses in the diode turn the stored energy into heat. Note that the voltage at the top of the resistor just before opening the switch was V (the battery voltage). After the switch opens this voltage drops to –0.65 volts as the diode turns on to carry the current. This rapidly changing voltage is characteristic of many types of switching supplies and is the reason they have a (deserved) reputation as Electromagnetic Interference Generators.

SWITCHING REGULATORS
The simplest form of switching regulator is the buck regulator. Look at the figure below and imagine that the switch has been closed for a very long time. Under these conditions, Vload will be equal to Vin. Therefore, this type of regulator can only produce an output voltage that is less than (or equal to) the input voltage. Now imagine the switch has been open for a long time. Vload will equal zero. These are the boundary conditions for this design.
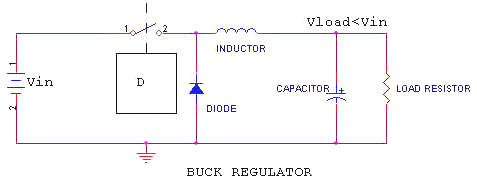
If things are linear, you might expect that if you closed the switch for half of the time and opened it for the other half, the output voltage (Vcap) would be (on average) Vin/2. You would be right. For this buck regulator there are only three design variables to worry about; the values of the inductor and capacitor and the switch frequency. This assumes a perfect switch, small parasitic resistors, and low stray capacitance in the inductor. These assumptions aren’t necessarily easy to arrange. There are formal analytic techniques that will produce a usable design, but let’s try for a seat of the pants feel for this application. We will ignore the feedback control and just look at the power flow. The topology of this circuit is very similar to the conventional series linear regulator that has been around forever. There are some interesting comparisons that can be made between the two.
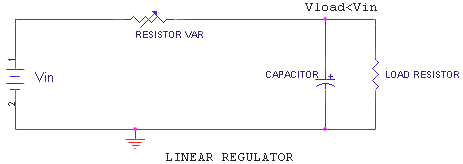
The variable resistor is the Series Pass Element in this linear regulator. If it is set to zero ohms or to infinity, the linear regulator will have the same boundary conditions as the buck switching regulator discussed earlier. For discussion, set its value to equal the Load Resistor. The voltage at the load will then be Vin/2, and the voltage drop across the series pass element will be the same. Therefore power loss in the series pass is the same as the load dissipation. This gives an efficiency of 50% and a warm series pass element. Note that if we could get a lossless voltage drop of Vin/2 at the series pass element, our regulator would be 100% efficient. Now go back to the stripped down buck regulator previously used as an example. Assume a current in the inductor that will produce Vin/2 volts across the load. If we run the switch at a 50% duty cycle (D=0.5) and at a frequency that only allows the current in the inductor to change by 1% during any one switch cycle we have a very close approximation to a lossless voltage drop. This works because the voltage across the inductor changes from +Vin/2 with the switch closed to –Vin/2 with the switch open (the inductor/diode junction drops to zero volts when the switch opens, remember?). Since the average voltage across the inductor is zero, the (average) current through the inductor won’t change (remember the inductor INTEGRATES the voltage across it). We now have our lossless voltage drop. Well, not really, since the inductor has a resistance and the switch and diode also have losses. But a lot closer than with the resistive series pass element in the linear regulator. Notice that a 50% duty cycle produces an output voltage of Vin/2. This generalizes to: Vload=Vin x D, no matter what the output load current is. This makes sense when you realize that there is no resistive series impedance except the (small as a percentage) inductor wire resistance. Of course the maximum current is limited by the I**2 R heating of the inductor wire and the saturation current of the inductor. To make this circuit useful, we usually need to add some type of regulation. The simplest is a fixed frequency Pulse Width Modulator that watches the output voltage and leaves the switch closed longer if the voltage falls below the Set Point and shorter if it rises above. This is, of course, the well known Negative Feedback concept. Which I won’t discuss further <smile>. That’s it. All you ever need to know about magnetic energy storage in an inductor, assuming you are trying to impress your supervisor, who was a business major. Of course, if you want to actually design a switcher from the component level up, you will need a bit more knowledge. Good luck and remember to clamp that inductor voltage.
Craig Taylor Jan 2004
![]()
In my previous tutorial (Magnetic Energy Storage) I spent some time discussing the fact that the inductors you buy or make don't really perform like the "ideal" inductor in the text book. That's too bad, because if they did the efficiency of switching supplies would improve quite a lot. This article is an attempt to describe the "non-idealness" of an inductor in such a way as to allow you to use the devices despite their many limitations.
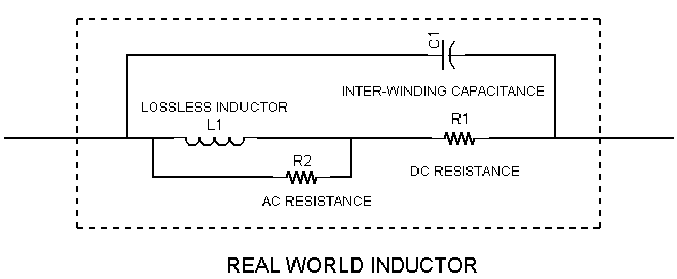
FIGURE 1
Figure 1 shows a schematic of an inductor model with most of the "real world" elements included. The three additions to the "pure inductor" schematic symbol are: AC resistance, DC resistance and stray (shunt) capacitance (the capacitor passes current around, or "shunts", the inductor). It's worth noting that the AC resistance is actually composed of two parts; core losses (magnetizing losses generating heat in the ferromagnetic core) and skin effect. Obviously, if you are dealing with an air core inductor, the core loss is zero.
The results of the two resistance type losses are fairly obvious (heat!), but the implications of the shunt capacitor are downright insidious. But first, where does the capacitance come from? You have to know the enemy to defeat him, after all. Since most power inductors are made by winding wire on a core, the obvious source is from two wires in close proximity. Actually, it's rather complicated. The wires can be adjacent turns that are side by side, or two turns on two different layers that end up on top of each other, or any and all combinations of those two. There can also be capacitance between the wire and the ferromagnetic core if it is one of those materials that is a reasonably good electrical conductor.
The summed capacitance, represented in the model by one ideal capacitor, is usually the result of many small capacitors in series and parallel combinations. The result is the same; stored energy in the capacitor when there is voltage across the inductor. The most obvious effect of this capacitance is to cause almost any inductor to have a Self-Resonant Frequency (SRF). If you look at the model and neglect the resistive type losses, you have a parallel LC circuit. One of the basic circuit equations says: frequency(resonance) = 1/ [2Pi sq root (LC)] Above this frequency, the inductor behaves like a capacitor and can't be used to store energy, at least not in the sense of a pure inductor. At one tenth the SRF, the inductor acts pretty much like an inductor; you can effectively ignore the capacitive effect. In between, you have to use nasty math to figure out what is going to happen, something I like to avoid. Something to always remember is that when using active switches in any design, the frequency of some energy components can be MUCH HIGHER than the switch cycling frequency.